ref: https://www.facebook.com/bhumisiam/posts/1299797980066324:0
สวัสดีครับแฟนเพจที่รักทุกท่าน
วันนี้ผมจะมาเล่าเนื้อหาต่อจากเมื่อวันก่อนที่ผผมค้างเพื่อนๆ เอาไว้ นั่นก็คือเรื่องสภาวะสมดุลในหน้าตัด คสล หรือ EQUILIBRIUM CONDITION IN RC SECTION นั่นเอง
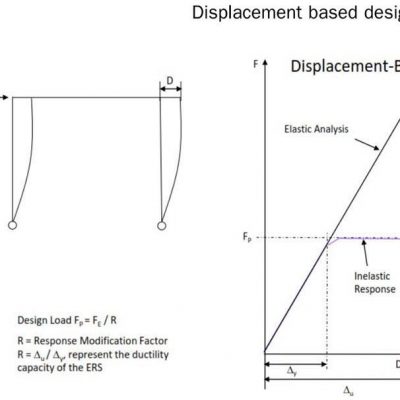
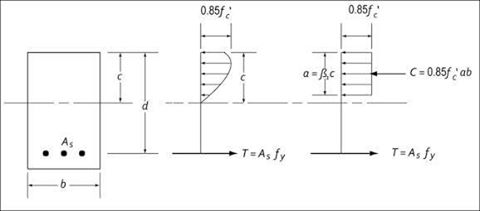
จากในรูปเดิมนะครับ ณ สภาวะการรับ นน ประลัยของโครงสร้าง เราจะมี สมมติฐานที่ว่าค่ากำลังต่างๆ ของวัสดุจะสูงขึ้นจนไปแตะที่ค่าขอบเขตสูงสุดเท่าที่จะเป็นไปได้ เช่น ค่าแรงเค้นอัดในคอนกรีต หรือ fc เราก็จะใช้เท่ากับ fc’ ที่ถูกทอนกำลังลงมาประมาณ 15% หรือ ค่ากำลังอัดประลัยที่อายุ 28 วัน ของคอนกรีต ค่าแรงเค้นดึงในเหล็ก หรือ fs ก็จะใช้เท่ากับ fy หรือ ค่ากำลังดึงที่จุดครากของเหล็กเสริม เป็นต้น
หากเราจะหาความสมดุลในหน้าตัดเราจะสามารถหาได้จากสมการสมดุลง่ายๆ นะครับ คือ
จากสมการสมดุลของแรงตามแนวแกน คือ แรงดึง เท่ากับ แรงอัด
∑N = 0
C – T = 0
C = T (1)
และจากสมการสมดุลของแรงโมเมนต์ คือ แรงดึง หรือ แรงอัด คูณกับแขนของแรง
∑M = 0
(C)(Z) – (T)(Z) = 0
M = (C)(Z) = (T)(Z) (2)
โดยที่ C = แรงอัดในคอนกรีต
C = (fc)(Ac) = (0.85 fc’)(a b) = 0.85 fc’ a b
และ T = แรงดึงในเหล็ก
T = (fs)(As) = (fy)(As) = fy As
ดังนั้นหากเราต้องการจะหาค่ากำลังโมเมนต์ที่หน้าตัดสามารถรับได้เราก็เพียงแค่คูณ ค่ากำลังดึง หรือ ค่ากำลังอัด กับแขนของแรง ซึ่งในที่นี้ก็เท่ากับระยะ Z หรือ ระยะ d ลบด้วยครึ่งหนึ่งของระยะ a หรือ a/2 จากในสมการที่ (2)
ดังนั้นในหนึ่งหน้าตัด หากเราทราบกำลังของวัสดุที่จะใช้ ทราบหน้าตัดคอนกรีตและเหล็กเสริมที่จะใช้ และ เราต้องการที่จะทราบค่าโมเมนต์ดัดที่หน้าตัดจะสามารถรับได้ เราก็แค่เริ่มต้นคำนวณหาค่า a ก่อน โดยที่ค่านี้หาได้จากสมการที่ (1) ได้ว่า
0.85 fc’ a b = fy As
ดังนั้น a = fy As / ( 0.85 fc’ a b )
ต่อมาเราก็จะแทนค่าต่างๆ ลงในสมการที่ (2) ได้ว่า
M = (T)(Z) = As fy (d – a/2)
โดยในสมการการหาค่าโมเมนต์ดัดของ ACI เราจะพบว่าใน CODE ได้กำหนดให้ค่าโมเมนต์ Mu เป็นค่าโมเมนต์ดัดประลัย และค่า Mn เป็นค่ากำลังโมเมนต์ระบุ หรือ Mn ที่ทำการคูณด้วยค่าแฟคเตอร์ลดกำลังรับแรงดัด หรือ REDUCTION FACTOR ไว้ด้วย ทั้งนี้ก็เพื่อจุดประสงค์ด้าน RELIABILITY ที่ดีของโครงสร้างนั่นเองครับ เราจะได้สมการในการหาแรงดัดของหน้าได้ใหม่เป็น
ØMn = Mu/Ø = ØAs fy (d -a/2)
ขอให้เพื่อนๆ วิศวกรทำความเข้าใจกันถึงสมการนี้ให้ดีๆ นะครับ เพราะเป็นสมการหนึ่งที่พวกเราชาวนักออกแบบทั้งหลายมักต้องใช้กันเป็นประจำ ขอให้โชคดีครับทุกๆ ท่าน
Today I’m going to continue the last issue we have already discussed that is the equilibrium condition in the RC section.
From the same figure at the ultimate stage loading we assumed that the strength of materials reaches it’s highest proportional limit i.e. the compressive stress in the concrete or fc we now use as fc’ which is reduced down by 15% of strength representing the ultimate strength at 28 days of age in concrete, tensile stress in the reinforced steel or fs we now use as fy representing the the yield strength of the reinforced steel etc.
If we take equilibrium in the section we now yield:
The equilibrium of normal force is equal between tension and compression
∑N = 0
C – T = 0
C = T (1)
and the equilibrium of moment force is also equal between the compression and tension forces multiply by the lever arm.
∑M = 0
(C)(Z) – (T)(Z) = 0
M = (C)(Z) = (T)(Z) (2)
Where; C = Compression force subjected to the concrete
C = (fc)(Ac) = (0.85 fc’)(a b) = 0.85 fc’ a b
and, T = Tension force subjected in the reinforced steel
T = (fs)(As) = (fy)(As) = fy As
Hence, if we want to compute the flexural strength in the section we just multiply the compression or tension force by the lever arm or in this place we use the Z value, or d minus half of the a distance, or a/2 from equation (2)
Thus, in one section if we know the strength of material used, we know the sectional area of the concrete and reinforced steel, and we now want to compute the nominal flexural strength of the section. We can just start from computing the value of a from equation (1)
0.85 fc’ a b = fy As
Hence, a = fy As / ( 0.85 fc’ a b )
Then we can use equation (2) to determine the flexural strength
M = (T)(Z) = As fy (d – a/2)
In the flexuar equation given from ACI we can see that the code use the expression of Mu which is the ultimate factored moment, and the Mn as the nominal moment, or the Mn divided by the reduction factor in order to make the section satisfy a good reliability condition. We now have the flexural equation equal to:
ØMn = Mu/Ø = ØAs fy (d -a/2)
Wishing all of you to understand this equation because we frequently use it in our beam design process. Good luck everyone.
หวังว่าความรู้เล็กๆ น้อยๆ ที่ผมได้นำมาฝากพี่แขก และ เพื่อนๆ ทุกๆ ท่านในวันนี้จะมีประโยชน์ต่อทุกๆ ท่านไม่มากก็น้อย และ จนกว่าจะพบกันใหม่
ADMIN JAMES DEAN
BSP-Bhumisiam
เสาเข็ม สปันไมโครไพล์ ช่วยแก้ปัญหาได้เพราะ
1) สามารถทำงานในที่แคบได้
2) ไม่ก่อให้เกิดมลภาวะทางเสียง
3) หน้างานสะอาด ไม่มีดินโคลน
4) สามารถรับน้ำหนักได้ 20-40 ตัน/ต้น
5) สามารถตอกชิดผนังกำแพง ไม่ทำให้โครงสร้างเดิมเสียหาย
สนใจติดต่อสินค้า เสาเข็ม ไมโครไพล์ (Micropile) สปันไมโครไพล์ (Spun MicroPile) มาตรฐาน มอก. ของ ภูมิสยาม ซัพพลาย ติดต่อ สายด่วน โทร 081-634-6586