สวัสดีครับแฟนเพจที่รักทุกๆ ท่าน
สืบเนื่องจากในสัปดาห์นี้น่าจะเป็นช่วงของการสอบไฟนอลของน้องๆ นักศึกษาหลายๆ คน ผมจึงอยากจะขอแทรกการโพสต์ในวันนี้ด้วยการตอบคำถามของน้องนักศึกษาท่านหนึ่งที่ตอนนี้กำลังอ่านหนังสือเพื่อเตรียมตัวสอบในวิชา ทฤษฎีโครงสร้าง โดยที่ผมได้ทำการสรุปใจความของปัญหาของน้องท่านนี้ได้ดังนี้ครับ
“ตอนนี้กำลังเจอกับปัญหาว่า หากผมมีความจำเป็นที่จะต้องทำการใช้วิธีการจำพวก GRAPHICAL METHOD เช่น วิธีการ CONJUGATE BEAM METHOD หรือวิธีการ MOMENT AREA METHOD เป็นต้น ผมจึงจำเป็นที่จะต้องนำเอาแผนภาพของแรงดัดหรือ BMD ไปสร้างเป็นกราฟ -M/EI หากผมเจอกรณีที่น้ำหนักบรรทุกนั้นเป็นแบบจุดหรือ CONCENTRATED LOAD ก็ไม่เท่าไหร่แต่หากเจอกับกรณีที่น้ำหนักบรรทุกนั้นเป็นแบบแผ่หรือ DISTRIBUTED LOAD ซึ่งกราฟ -M/EI จะมีรูปทรงเป็น PARABOLIC ยกกำลัง 2 ขึ้นไป สำหรับกรณีหาพื้นที่นั้นยังไม่หนักหนาแต่สำหรับกรณีที่ผมจะทำการคำนวณหาตำแหน่งของค่า X ที่ค่า ROTATION นั้นมีค่าเท่ากับ 0 รูปมันจะคำนวนหาค่า X ได้อย่างไรดีครับ ?”
หากน้องหรืออาจจะมีเพื่อนๆ ในเพจท่านใดท่านหนึ่งต้องเจอเข้ากับปัญหาในลักษณะนี้ ผมขอให้คำแนะนำดังนี้นะครับ
- ให้น้องเปลี่ยนไปใช้วิธีการจำพวก NON- GRAPHICAL METHOD เช่น วิธีการ DOUBLE INTEGRATION หริอวิธีการ VIRTUAL WORK หรือวิธีการ CASTIGLIANO’S 2ND THEOREM เป็นต้น เพราะว่าวิธีการเหล่านี้ เราจะอาศัยการสร้างสมการโมเมนต์ดัดแทนที่การวาดรูปแผนภาพของแรงดัด ซึ่งก็จะช่วยลดความผิดพลาดที่อาจจะเกิดขึ้นจากการวาดรูปผิดได้นะครับ
- หากน้องยืนยันว่าจำเป็นที่จะต้องใช้วิธีการจำพวก GRAPHICAL METHOD เหล่านี้จริงๆ เราก็จะต้องแก้ปัญหาโดยการนำเอาค่าต่างๆ ที่อยู่บนแผนภาพแรงเฉือนหรือ SFD ที่เรามักจะนำมาใช้ในการคำนวณหาพื้นที่เพื่อที่จะนำเอาไปสร้างแผนภาพของแรงดัด โดยที่เราจะต้องสร้างให้ค่าๆ นี้อยู่ในรูปแบบของฟังก์ชั่น W(X) นะครับ
เรามาดูตัวอย่างสั้นๆ เพื่อใช้ประกอบคำอธิบายในโพสต์ๆ นี้ให้เกิดความเข้าใจที่กระจ่างยิ่งขึ้นกันสักเล็กน้อยก็แล้วกันนะครับ
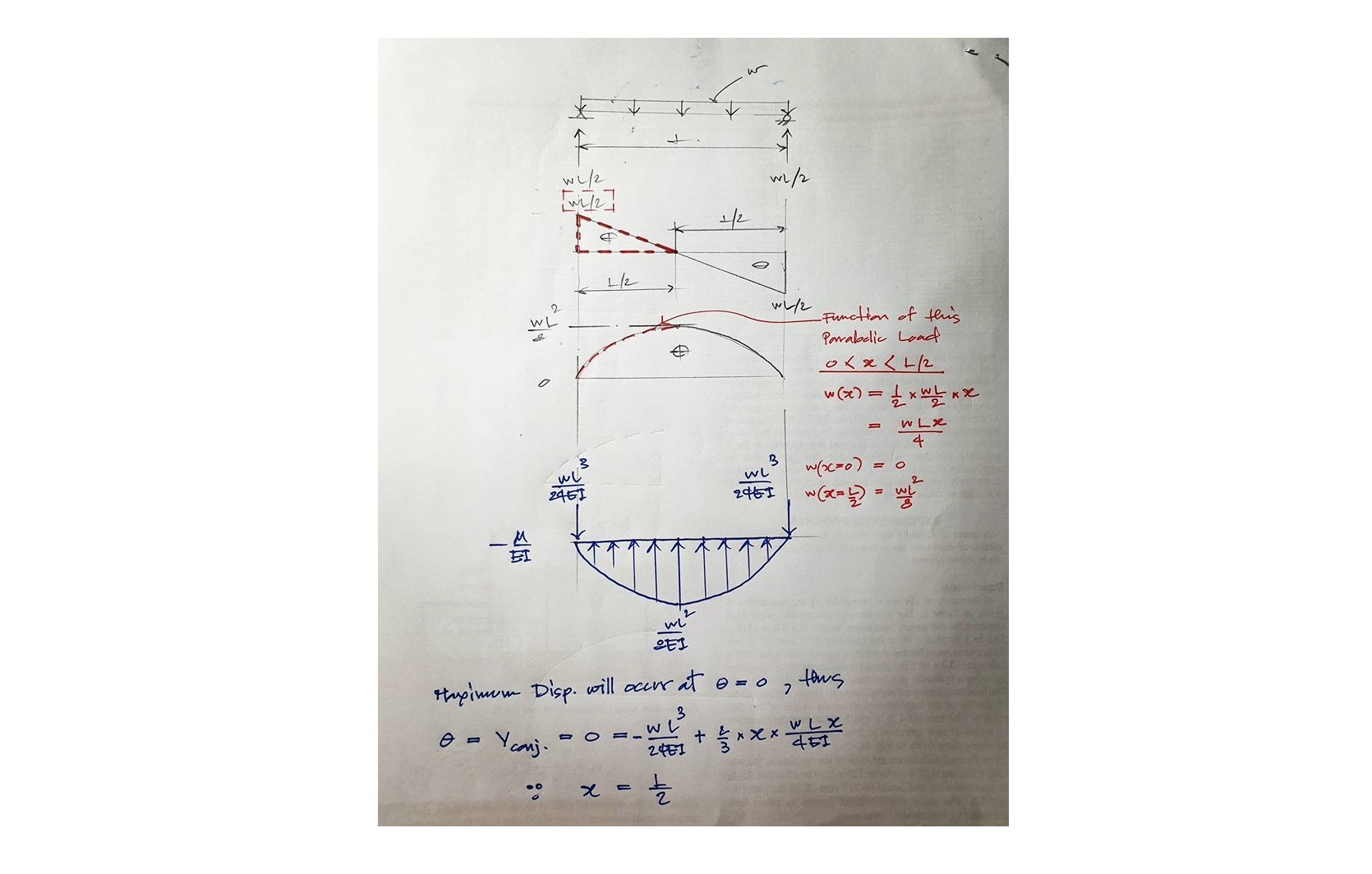
จากรูปเป็นปัญหาโครงสร้างคานช่วงเดียวอย่างง่ายๆ หรือ SIMPLE BEAM ที่รับน้ำหนักกระทำแบบแผ่กระจายตัวสม่ำเสมอหรือ UNIFORMLY DISTRIBUTED LOAD และในเมื่อลักษณะของการรับน้ำหนักของคานๆ นี้เป็นการรับน้ำหนักที่มีความสมมาตร เราก็จะทราบกันดีอยู่แล้วว่า ค่าการโก่งตัวสูงสุดหรือ MAXIMUM DEFLECTION ของโครงสร้างคานในลักษณะแบบนี้จะเกิดขึ้นที่ตำแหน่งกึ่งกลางของคานหรือระยะ X เท่ากับ L/2 จากปลายซ้ายมือของคานแต่ที่ผมเลือกนำเอาปัญหาข้อนี้มาใช้เป็นตัวอย่างก็เพราะเพื่อนๆ น่าจะคุ้นเคยและก็ทราบข้อเท็จจริงเหล่านี้กันดีอยู่แล้วนะครับ
พอเราทำการสร้าง CONJUGATE LOAD บน CONJUGATE BEAM เสร็จเราก็จะทำการ TAKE MOMENT รอบจุดรองรับที่ด้านขวามือสุดของคาน ก็จะทำให้สามารถทราบค่าแรงปฏิกิริยาของจุดรองรับที่ปลายซ้ายมือสุดของคานซึ่งจะมีค่าเท่ากับ
∑M = 0 (COUNTER CLOCK WISE IS +)
(L)(V) – (2/3)(WL^(2)/8EI)(L)(L/2) = 0
(L)(V) – WL^(4)/24EI) = 0
(L)(V) = WL^(4)/24EI)
V = WL^(3)/24EI) ↓
ต่อมาคือ เราทราบจากหลักการของ CURVATURE ว่าเทอมของ V เทอมของ M เทอมของ θ และเทอมของ ∆ นั้นจะมีความสัมพันธ์ซึ่งกันและกันจาก
dV/dx = – W(X)
dM/dx = V
(EI) d^(2)y/dx^(2) = M
(EI) dy/dx = θ
(EI) y = ∆
ดังนั้นเราจะเลือกนำเอาความสัมพันธ์ข้างต้นนี้มาใช้ซึ่งก็คือ พื้นที่ของค่า SFD จะมีค่าเท่ากับค่าบนกราฟ BMD นั่นก็คือจากรูป SFD เริ่มต้นที่ช่วงแรกก่อนซึ่ง X มีค่ามากกว่า 0 แต่ X ก็มีค่าน้อยกว่า L/2 หากเราต้องการที่จะทราบค่าบน BMD โดยที่ให้ติดอยู่ในรูปฟังก์ชั่นของค่า X เราก็จะสามารถทำการคำนวณได้ว่า
W(X FOR 0 ≤ X ≤ L/2) = (1/2) (WL/2) (X)
W(X FOR 0 ≤ X ≤ L/2) = WLX/4
ซึ่งพอเรานำเอารูปของ BMD นี้ไปสร้างเป็น CONJUGATE LOAD บน CONJUGATE BEAM เราก็จะได้ค่า W(X) ออกมาเท่ากับ
W(X FOR 0 ≤ X ≤ L/2) = WLX/4EI
ดังนั้นหากเราต้องการที่จะทราบค่า MAXIMUM DEFLECTION เราก็ต้องทำการคำนวณหาว่า ณ ตำแหน่งใดที่ค่าของ ROTATION นั้นมีค่าเท่ากับ ศูนย์ เราก็ทำการตั้งสมการขึ้นมา โดยมีข้อแม้เพียงว่า สมการนี้จะใช้ได้เฉพาะช่วงของ X มีค่ามากกว่า 0 แต่ X ก็มีค่าน้อยกว่า L/2 ดังนั้น
θ = SHEAR ON CONJUGATE BEAM = 0
0 = -WL^(3)/24EI + (2/3) (X) W(X)
0 = -WL^(3)/24EI + (2/3) (X) WLX/4EI
0 = -WL^(3)/24EI + 2WLX^(2)/12EI
0 = -L^(2)/24 + X^(2)/6
X^(2)/6 = L^(2)/24
X^(2) = L^(2)/4
X = √[ L^(2)/4 ]
X = L/2
ยังไงผมก็ขออำนวยอวยพรให้แก่น้องๆ ทุกคน ให้สามารถที่จะทำข้อสอบในส่วนของการสอบไฟนอลที่กำลังมาถึงนี้ ให้ผ่านพ้นไปได้ด้วยดีทุกๆ คนนะครับ
หวังว่าความรู้เล็กๆ น้อยๆ ที่ผมได้นำมาฝากแก่เพื่อนๆ ทุกๆ ท่านจากคำถามในวันนี้น่าที่จะมีประโยชน์ต่อทุกๆ ท่านไม่มากก็น้อย และ จนกว่าจะพบกันใหม่นะครับ
#โพสต์ของวันพุธ
#แนะนำนักศึกษาเรื่องวิธีในการคำนวณหาตำแหน่งที่ค่าการโก่งตัวนั้นเกิดขึ้นสูงที่สุด
ADMIN JAMES DEAN
บริษัท ภูมิสยาม ซัพพลาย จำกัด ผู้นำกลุ่มธุรกิจเสาเข็มสปัน ไมโครไพล์ รายแรกและรายเดียวในประเทศไทย ที่ได้การรับรองมาตรฐาน ISO 45001:2018 การจัดการอาชีวอนามัยและความปลอดภัย การให้บริการตอกเสาเข็ม The Provision of Pile Driving Service และได้รับการรับรอง ISO 9001:2015 ของระบบ UKAS และ NAC รายแรกและรายเดียวในประเทศไทย ที่ได้รับการรับรองระบบบริหารงานคุณภาพ ตามมาตรฐานในกระบวนการ การออกแบบเสาเข็มสปันไมโครไพล์ การผลิตเสาเข็มสปันไมโครไพล์ และบริการตอกเสาเข็มเสาเข็มสปันไมโครไพล์ (Design and Manufacturing of Spun Micropile/Micropile and Pile Driving Service) Certified by SGS (Thailand) Ltd.
บริษัท ภูมิสยาม ซัพพลาย จำกัด คือผู้ผลิตรายแรกและรายเดียวในไทย ที่ได้รับการรับรองคุณภาพ Endoresed Brand จาก SCG ด้านการผลิตเสาเข็ม สปันไมโครไพล์ และได้รับเครื่องหมาย มาตรฐาน อุตสาหกรรม มอก. 397-2524 เสาเข็มสปันไมโครไพล์ Spun Micro Pile พร้อมรับประกันผลงาน และความเสียหายที่เกิดจากการติดตั้ง 7+ Year Warranty เสาเข็มมีรูกลมกลวงตรงกลาง การระบายดินทำได้ดี เมื่อตอกแล้วแรงสั่นสะเทือนน้อยมาก จึงไม่กระทบโครงสร้างเดิม หรือพื้นที่ข้างเคียง ไม่ต้องขนดินทิ้ง ตอกถึงชั้นดินดานได้ ด้วยเสาเข็มคุณภาพมาตรฐาน มอก. การผลิตที่ใช้เทคโนโลยีที่ทันสมัย จากประเทศเยอรมัน เสาเข็มสามารถทำงานในที่แคบได้ หน้างานสะอาด ไม่มีดินโคลน เสาเข็มสามารถรับน้ำหนักปลอดภัยได้ 15-50 ตัน/ต้น ขึ้นอยู่กับขนาดเสาเข็มและสภาพชั้นดิน แต่ละพื้นที่ ทดสอบโดย Dynamic Load Test ด้วยคุณภาพและการบริการที่ได้มาตรฐาน เสาเข็มเราจึงเป็นที่นิยมในงานต่อเติม
รายการเสาเข็มภูมิสยาม
1. สี่เหลี่ยม S18x18 cm.
รับน้ำหนัก 15-20 ตัน/ต้น
2. กลม Dia 21 cm.
รับน้ำหนัก 20-25 ตัน/ต้น
3. กลม Dia 25 cm.
รับน้ำหนัก 25-35 ตัน/ต้น
4. กลม Dia 30 cm.
รับน้ำหนัก 30-50 ตัน/ต้น
(การรับน้ำหนักขึ้นอยู่กับสภาพชั้นดินในแต่ละพื้นที่)

082-790-1447
082-790-1448
082-790-1449
091-947-8945
081-634-6586
? Web:
bhumisiam.com
micro-pile.com
spun-micropile.com
microspunpile.com
bhumisiammicropile.com