สวัสดีครับแฟนเพจที่รักทุกๆ ท่าน
กลับมาพบกันในทุกๆ วันเสาร์แบบนี้อีกครั้งหนึ่งซึ่งผมก็จะมาพบกับเพื่อนๆ เพื่อที่จะพูดคุยกันถึงหัวข้อ “ถาม-ตอบชวนสนุก” กันนะครับ
โดยที่ในวันนี้ผมได้ทำการหยิบยกเอาคำถามที่มีความเกี่ยวข้องกันกับเรื่อง ความรู้ดีๆ เพื่อคุณผู้หญิง เอามาเป็นคำถามประจำสัปดาห์เพื่อให้มีความต่อเนื่องจากคำถามในสัปดาห์ที่แล้วด้วยและเหมือนเช่นเคยผมคงจะต้องออกตัวอีกครั้งหนึ่งว่า คำถามประจำสัปดาห์นี้สุดแสนจะง่ายมากๆๆๆๆๆๆๆๆๆ โดยที่โจทย์ในวันนี้ก็คือ
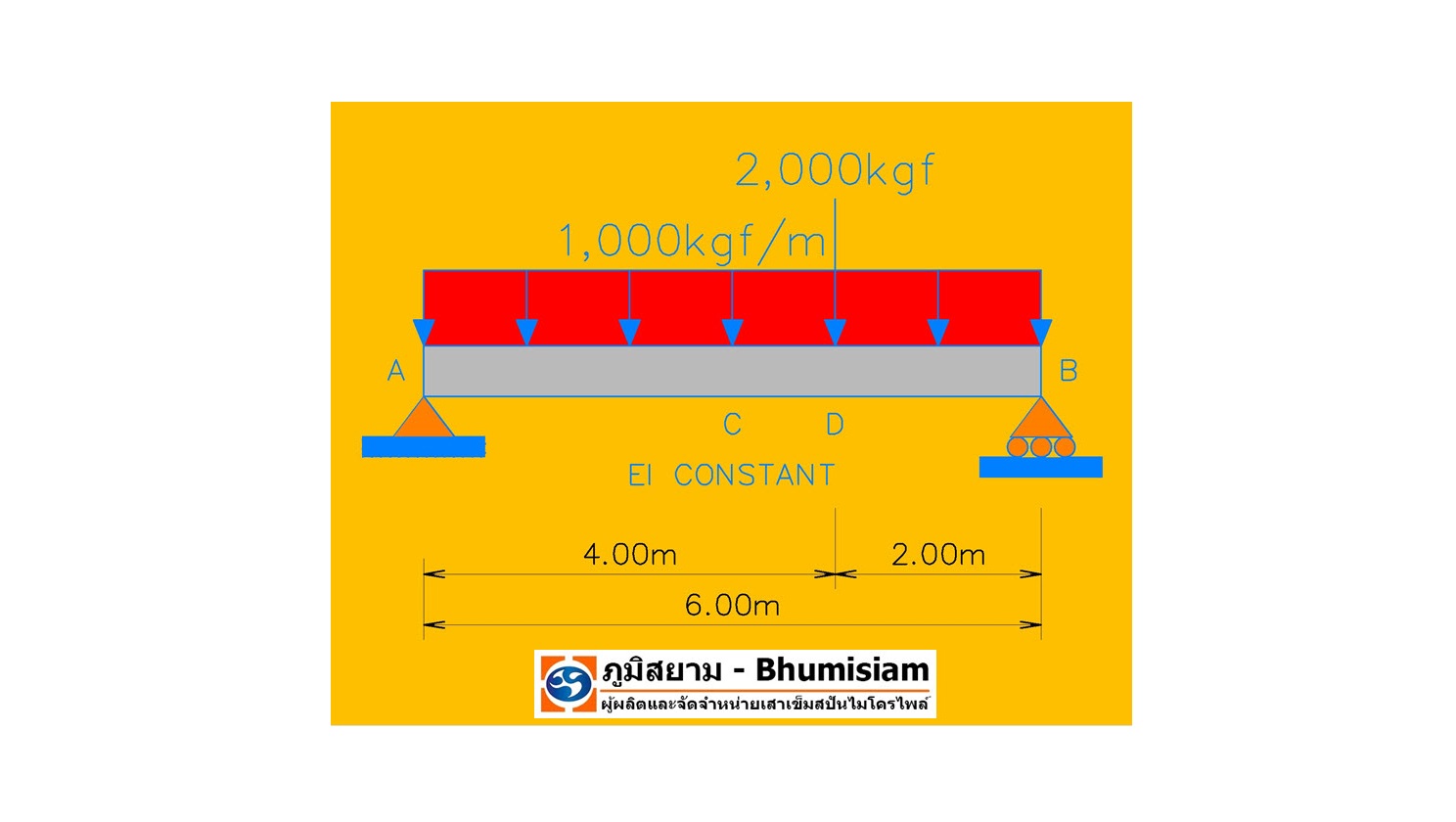
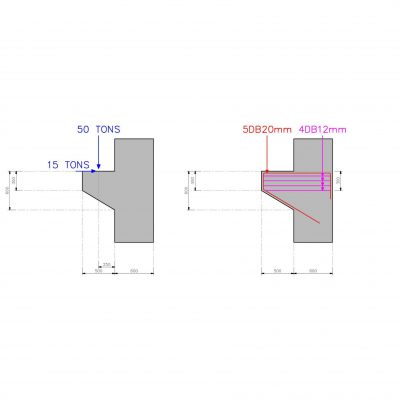
หากผมมีคานรับแรงดัดที่จะต้องรับน้ำหนักบรรทุกดังที่ได้แสดงอยู่ในรูป โดยคานจะต้องรับน้ำหนักบรรทุกแบบกระทำโดยแผ่กระจายตัวสม่ำเสมอหรือ UNIFORMLY DISTRIBUTED LOAD มีค่าเท่ากับ 1,000 กิโลกรัมต่อเมตร และ จะต้องรับน้ำหนักบรรทุกแบบกระทำเพียงจุดเดียวหรือ CONCENTRATED LOAD มีค่าเท่ากับ 2,000 กิโลกรัม ทั้งนี้คานรับแรงดัดของเรานั้นจะมีความยาวช่วงเท่ากับ 6.00 เมตร และทำจากเหล็กรูปพรรณที่มีค่าโมดูลัสยืดหยุ่นเท่ากับ 2×10^(6) กิโลกรัมต่อตารางเซนติเมตร และ มีค่าโมดูลัสความเฉื่อยของหน้าตัดเท่ากับ 10,000 ซม^(4)
จงทำการคำนวณดูซิว่า คานรับแรงดัดของเรานั้นจะมีค่าการโก่งตัว “สูงสุดที่สุด” ของคานเท่ากับเท่าใด และ ตำแน่งดังกล่าวนั้นจะเกิดขึ้นที่ตำแหน่งใดครับ ?
#โพสต์ของวันเสาร์
#ถามตอบชวนสนุก
#ปัญหาเรื่องการคำนวณหาค่าการโก่งตัวของคานรับแรงดัด
#การคำนวณหาค่าการโก่งตัวค่าสูงสุดของคาน
เฉลย
ก่อนอื่นเลยผมคิดว่าก่อนที่พวกเราจะมาดูคำตอบของปัญหาข้อนี้กัน สิ่งแรกที่อาจจะผุดขึ้นมาในสมองของเพื่อนๆ เมื่อได้ยินคำถามๆ นี้ก็คงจะเป็น
“แล้วเจ้าตำแหน่งจุด “กึ่งกลาง” ของคานรับแรงดัด ซึ่งผมได้ทำการตั้งเป็นำถามไปแล้วในสัปดาห์ที่ผ่านมานี่ มันไม่ใช่ค่าการโก่งตัว “สูงที่สุด” หรือ ?”
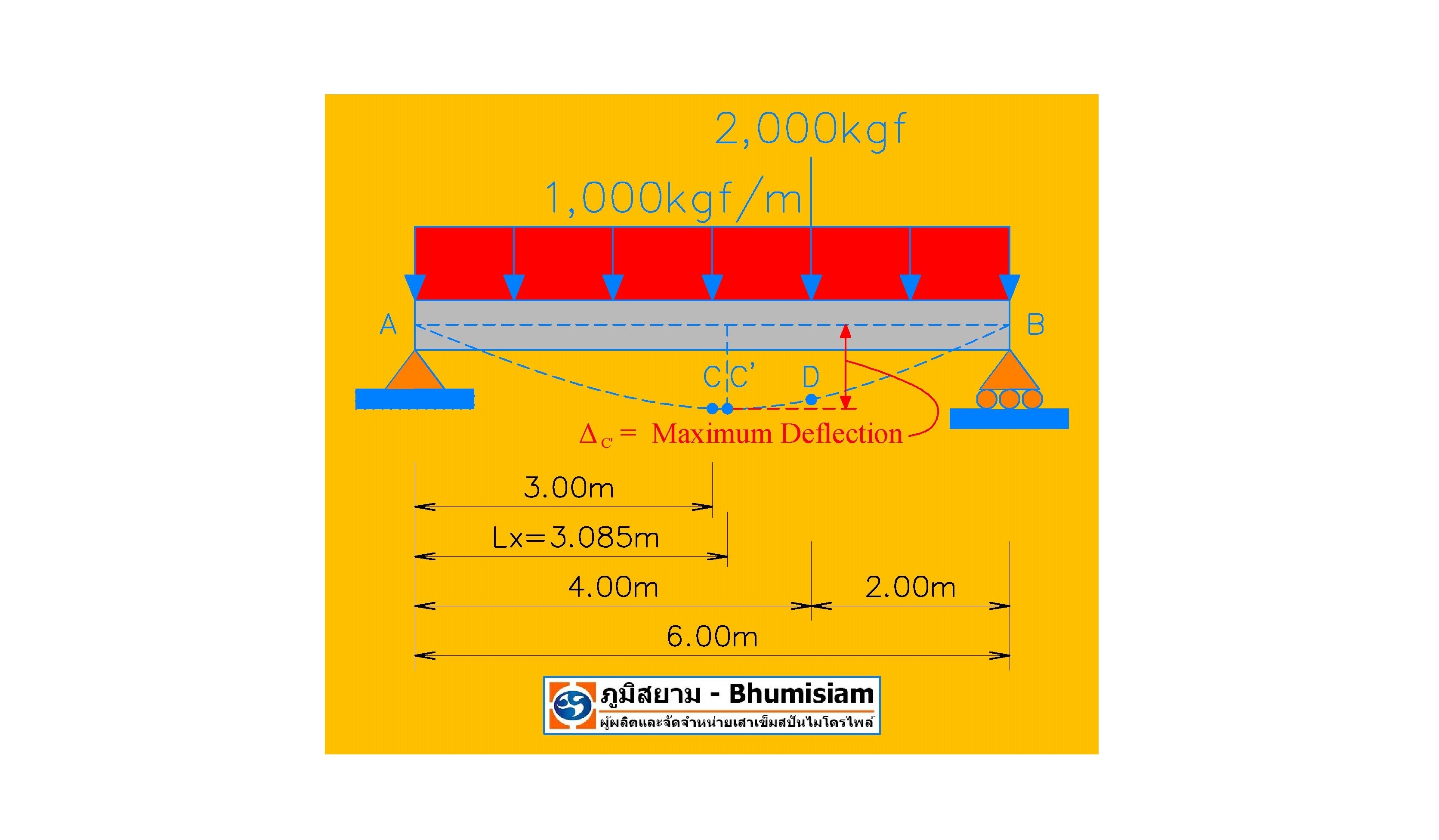
คำตอบคือ “ไม่ใช่” แต่ ก็ใกล้เคียงมากๆๆๆๆๆ เอาเป็นว่าวันนี้เรามาดูคำตอบข้อนี้ไปพร้อมๆ กันจะดีกว่าและจากประโยคข้างต้นนี้เอง ผมจึงอยากจะขอบอกเอาไว้ก่อนเลยว่า ตำแหน่งที่คานนั้นจะเกิดค่าการโก่งตัวสูงสุดย่อมไม่ใช่ที่ตำแหน่งระยะ “3.000 เมตร” (จากปลายซ้ายมือของคาน) แต่จะเป็นที่ระยะ “3.085 เมตร” (จากปลายซ้ายมือของคาน) นะครับ
ดังนั้นผมว่าเรามาเริ่มต้นทำการพิจารณาไปทีละกรณีว่าเพราะเหตุใดผมจึงได้ทำการระบุไว้ว่าคานจะมีค่าการโก่งตัวสูงสุด ณ ตำแหน่งนี้ โดยที่เราอาจจะเริ่มต้นจากกรณีที่ 4 หรือกรณีของการที่คานจะต้องทำหน้าที่ในการรับน้ำหนักบรรทุกแบบกระทำเพียงจุดเดียว สำหรับปัญหาข้อนี้เราจะทราบได้จากข้อมูลในตารางว่า ระยะที่จะเกิดค่าการโก่งตัวสูงสุดนั้นจะเกิดที่ระยะ
Lx (case 4) = √[L^(2) – b^(2)]/3
ซึ่งหากทำการแทนค่าด้วย L เท่ากับ 6.000 เมตร และ b เท่ากับ 2.000 เมตร ลงไปในสมการๆ นี้ก็จะได้ค่าของ Lx ออกมามีค่าเท่ากับ
Lx (case 4) = √{[6^(2) – 2^(2)]/3}
Lx (case 4) = √{[32]/3}
Lx (case 4) = 3.266 เมตร (จากปลายซ้ายมือของคาน)
ต่อมาเราก็จะมาดูในกรณีที่ 4 หรือกรณีของการที่คานจะต้องทำหน้าที่ในการรับน้ำหนักบรรทุกแบบกระทำโดยแผ่กระจายตัวสม่ำเสมอกันบ้าง สำหรับปัญหาข้อนี้เราจะทราบได้ดีเลยว่า ค่าการโก่งตัวสูงสุดของคานสำหรับกรณีๆ นี้จะอยู่ที่ตำแหน่งจุดกึ่งกลางของคานหรือพูดง่ายๆ ก็คือ
Lx (case 5) = L / 2
Lx (case 5) = 6.000 / 2
Lx (case 5) = 3.000 เมตร (จากปลายซ้ายมือของคาน)
หลังจากที่เราทราบผลแล้วภายหลังจากการที่เราได้ทำการพิจารณาไปทีละกรณีไปเรียบร้อยแล้วว่า Lx ของ case 4 นั้นจะมีค่าเท่ากับ 3.266 เมตร (จากปลายซ้ายมือของคาน) และ Lx ของ case 5 นั้นจะมีค่าเท่ากับ 3.000 เมตร (จากปลายซ้ายมือของคาน) เมื่อเราทำการรวมผลหรือ COMBINE ระหว่าง case 4 และ case 5 เข้าด้วยกันตามหลักการ SUPERPOSITION แล้วเพื่อนๆ คิดว่า ระยะของ Lx ของรูปที่ทำการรวมผลนั้นจะมีค่าเป็นอย่างไรครับ ?
คำตอบก็จะค่อนข้างง่ายๆ ตรงไปตรงมาและค่อนข้างที่จะมีความสอดคล้องกันกับข้อเท็จจริงสำหรับกรณีของโครงสร้างคานของเรานั่นก็คือ
Lx (case 5) < Lx (combine) < Lx (case 4)
นั่นเป็นเพราะเมื่อผลจากแต่ละกรณีนั้นมีค่าที่แตกต่างกันออกไป ค่าหนึ่งมาก (3.266 เมตร) อีกค่าหนึ่งน้อย (3.000 เมตร) ก็จะส่งผลทำให้ผลรวมของรูปที่ได้ทำการรวมผลไปนั้นเปลี่ยนแปลงไปด้วยโดยที่สำหรับกรณีนี้ก็อย่างที่ผมได้แจ้งไปว่าระยะค่าการโก่งตัวสูงสุดของเรานั้นจะเกิดขึ้นระหว่างค่าทั้งสอง (3.085 เมตร) ดังนั้นเราก็จะสามารถทำการคำนวณหาค่าการโก่งตัวของคาน ณ ตำแหน่งนี้ได้โดยการแทนค่าต่างๆ ลงไปในสมการที่ได้ให้ไว้ในตาราง โดยที่คำตอบก็จะมีค่าเท่ากับ
Δ(c’) = Δ(c’ case 5) + Δ(c’ case 6)
Δ(c’) = – W [x^(4) – 2 L x^(3) + L^(3) x]/(24EI) + Pb {x^(3) – [L^(2) – b^(2)]x}/(6EIL)
Δ(c’) = 100 x { – 1000 [3.085^(4) – 2 x 6 x 3.085^(3) + 6^(3) x 3.085]/(24 x 2 x 10^(10) x 0.0001) + 2000 x 2 {3.085^(3) – [6^(2) – 2^(2)] x 3.085}/(6 x 2 x 10^(10) x 0.0001 x 6) }
Δ(c’) = – 0.843 – 0.385
Δ(c’) = -1.228 cm
ซึ่งหากเพื่อนๆ ยังจำกันได้จากปัญหาในสัปดาห์ที่แล้วที่คำตอบของค่าการโก่งตัวของคาน ณ ตำแหน่งกึ่งกลางของคานนั้นจะมีค่าเท่ากับ
Δ(c) = -1.227 cm
ซึ่งก็จะเป็นไปตามที่ผมได้แจ้งกับเพื่อนๆ ไปในตอนต้นแล้วว่าถึงตำแหน่งๆ นี้จะ “ไม่ใช่” ค่าสูงสุด แต่ ก็ถือได้ว่ามีความใกล้เคียงมากๆ เลยใช่มั้ยละครับ
ผมว่าเรามาทำการสรุปสิ่งต่างๆ ที่เราเรียนรู้ได้จากการแก้ปัญหาข้อนี้กันพอสังเขป เราก็อาจจะสามารถทำการสรุปออกมาได้เป็น 2 ข้อหลักๆ ซึ่งก็จะประกอบไปด้วย
- เพื่อนๆ จะเห็นได้ถึงความสำคัญของการวิเคราะห์หาค่าการโก่งตัว ณ จุด “กึ่งกลาง” ของช่วงของโครงสร้างคาน ถึงแม้ว่าปัญหาของเราจะมีรูปแบบของแรงรูปแบบใดๆ ก็ตามแต่และเราได้ทำการคำนวณหาค่าการเสียรูปสูงสุดนั้นๆ ออกมาได้แล้ว หากเราทำการวิเคราะห์หาค่าของการเสียรูป ณ ตำแหน่งจุดกึ่งกลางของคานออกมาได้ เราก็จะพบว่าค่าทั้งสองนี้จะมีความใกล้เคียงกันมากๆ จนอาจจะเรียกได้ว่า ค่าของการเสียรูปของโครงสร้าง ณ จุดกึ่งกลางคานนี้อาจจะเป็นตัวแทนของค่าการเสียรูปที่เกิดขึ้นภายในโครงสร้างคานเลยก็ได้นะครับ
- เมื่อเกิดการรวมผลกันระหว่างแรงที่มีลักษณะแตกต่างกันตั้งแต่สองรูปแบบขึ้นไป ตำแหน่งที่จะเกิดค่าการเสียรูปสูงสุดของโครงสร้างที่เราได้ทำการรวมผลจะเกิดขึ้นโดยอยู่ที่ตำแหน่ง “ระหว่าง” ตำแหน่งของค่าการเสียรูปสูงสุดของรูปแบบแรงหนึ่งๆ กับตำแหน่งของค่าการเสียรูปสูงสุดของอีกรูปแบบแรงหนึ่งๆ “เสมอ” เลยนะครับ
ในตอนท้ายนี้สำหรับเพื่อนๆ ที่อาจจะมีความสงสัยและทำการตั้งคำถามกับผมว่า
“ผมทราบได้อย่างไรว่า สำหรับปัญหาข้อนี้คานของเราจะมีค่าการโก่งตัวสูงสุด ณ ตำแหน่ง Lx เท่ากับ 3.085 เมตร (จากปลายซ้ายมือของคาน) ?”
ผมขออนุญาตอุบเอาไว้ก่อนเพราะผมอยากจะให้ติดตามกันต่อในวันอังคารนี้ โดยที่ผมจะทำการอธิบายเพิ่มเติมโดยที่จะอ้างอิงมาที่ปัญหาข้อนี้ด้วย หากเพื่อนๆ ท่านใดที่มีความสนใจอยากที่จะทราบและทำความเข้าใจเพิ่มเติม ก็สามารถที่จะติดตามอ่านบทความฉบับนี้ของผมกันได้ในวันอังคารหน้าที่จะถึงนี้นะครับ
หวังว่าความรู้เล็กๆ น้อยๆ ที่ผมได้นำมาฝากแก่เพื่อนๆ ทุกๆ ท่านจากคำตอบในวันนี้น่าที่จะมีประโยชน์ต่อทุกๆ ท่านไม่มากก็น้อย และ จนกว่าจะพบกันใหม่นะครับ
#โพสต์ของวันอาทิตย์
#ถามตอบชวนสนุก
#ตอบปัญหาเรื่องการคำนวณหาค่าการโก่งตัวของคาน
#เฉลยปัญหาการคำนวณหาค่าการโก่งตัวค่าสูงสุดของคาน
ADMIN JAMES DEAN
บริษัท ภูมิสยาม ซัพพลาย จำกัด ผู้นำกลุ่มธุรกิจเสาเข็มสปัน ไมโครไพล์ รายแรกและรายเดียวในประเทศไทย ที่ได้การรับรองมาตรฐาน ISO 45001:2018 การจัดการอาชีวอนามัยและความปลอดภัย การให้บริการตอกเสาเข็ม The Provision of Pile Driving Service และได้รับการรับรอง ISO 9001:2015 ของระบบ UKAS และ NAC รายแรกและรายเดียวในประเทศไทย ที่ได้รับการรับรองระบบบริหารงานคุณภาพ ตามมาตรฐานในกระบวนการ การออกแบบเสาเข็มสปันไมโครไพล์ การผลิตเสาเข็มสปันไมโครไพล์ และบริการตอกเสาเข็มเสาเข็มสปันไมโครไพล์ (Design and Manufacturing of Spun Micropile/Micropile and Pile Driving Service) Certified by SGS (Thailand) Ltd.
บริษัท ภูมิสยาม ซัพพลาย จำกัด คือผู้ผลิตรายแรกและรายเดียวในไทย ที่ได้รับการรับรองคุณภาพ Endoresed Brand จาก SCG ด้านการผลิตเสาเข็ม สปันไมโครไพล์ และได้รับเครื่องหมาย มาตรฐาน อุตสาหกรรม มอก. 397-2524 เสาเข็มสปันไมโครไพล์ Spun Micro Pile พร้อมรับประกันผลงาน และความเสียหายที่เกิดจากการติดตั้ง 7+ Year Warranty เสาเข็มมีรูกลมกลวงตรงกลาง การระบายดินทำได้ดี เมื่อตอกแล้วแรงสั่นสะเทือนน้อยมาก จึงไม่กระทบโครงสร้างเดิม หรือพื้นที่ข้างเคียง ไม่ต้องขนดินทิ้ง ตอกถึงชั้นดินดานได้ ด้วยเสาเข็มคุณภาพมาตรฐาน มอก. การผลิตที่ใช้เทคโนโลยีที่ทันสมัย จากประเทศเยอรมัน เสาเข็มสามารถทำงานในที่แคบได้ หน้างานสะอาด ไม่มีดินโคลน เสาเข็มสามารถรับน้ำหนักปลอดภัยได้ 15-50 ตัน/ต้น ขึ้นอยู่กับขนาดเสาเข็มและสภาพชั้นดิน แต่ละพื้นที่ ทดสอบโดย Dynamic Load Test ด้วยคุณภาพและการบริการที่ได้มาตรฐาน เสาเข็มเราจึงเป็นที่นิยมในงานต่อเติม
รายการเสาเข็มภูมิสยาม
1. สี่เหลี่ยม S18x18 cm.
รับน้ำหนัก 15-20 ตัน/ต้น
2. กลม Dia 21 cm.
รับน้ำหนัก 20-25 ตัน/ต้น
3. กลม Dia 25 cm.
รับน้ำหนัก 25-35 ตัน/ต้น
4. กลม Dia 30 cm.
รับน้ำหนัก 30-50 ตัน/ต้น
(การรับน้ำหนักขึ้นอยู่กับสภาพชั้นดินในแต่ละพื้นที่)

082-790-1447
082-790-1448
082-790-1449
091-947-8945
081-634-6586
? Web:
bhumisiam.com
micro-pile.com
spun-micropile.com
microspunpile.com
bhumisiammicropile.com